FLOW NETS

A flow line is defined as a line such that the macroscopic velocity vector is tangent to it. For specified boundary conditions flow lines and equipotential lines can be mapped in two dimensions to form a flow net. The two sets of lines form an orthogonal pattern of small squares. In a few simplified cases, the differential equation governing flow can be solved to obtain the flow net. Generally, however, graphical solutions, based on trial and error approximation or laboratory model studies are necessary.

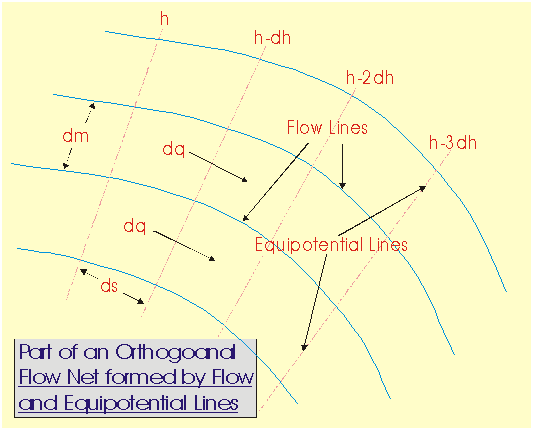
Let us consider the position of a flow net shown in the figure below. The hydraulic gradient ‘i’ is given by

dh

i = -------- (i)

ds

where ds = separation of equipotential lines and dh = hydraulic height, and the constant flow q, between two adjacent flow lines, is given by

dh

q = K dm ----------- -(ii)

ds

Where K= Permeability constant (Hydraulic conductivity), and dm = Seperation of flow lines

for unit thickness. But for a square of flow net,

ds @ dm then equation ( ii) reduces to

q = Kdh -------------(iii)

Applying this to entire flow net where the total head loss ‘h’ is divided into ‘n’ squares between any two adjacent flow lines, then

h

dh --------( iv)

n

If the flow is divided into’ m’ channels by flow lines, then the total flow,

Q = mq = Kdhm

=Khm/n, Proved

Q = mq = Kmh/n

Thus, the geometry of the flow net, together with the permeability and head loss, enables to total flow in section to be computed directly.